Время от времени мы видим шквал новостей о квантовых вычислениях. Этой теме уделяется очень много внимания: одна компания заявила, что у нее есть алгоритм шифрования, который вам скоро понадобится, так как квантовые компьютеры делают современные алгоритмы шифрования бесполезными.

У человека любознательного такие заявления вызывают вопросы. Что такое квантовые вычисления (рисунок 1)? Это реально? Если да, то как это работает? И как это связано с криптографией? Затем появляются более личные вопросы. Могут ли квантовые вычисления изменить мои методы проектирования? Должен ли я изучить этот материал?

Даже в визуализации художников квантовые вычислительные элементы не похожи ни на что из цифрового аппаратного мира.

Оказывается, это не слишком простые вопросы для изучения. Соответствующая литература в основном относится к одному из двух жанров. Первый предназначен для широкой читательской аудитории и рассматривает квантовую механику как чертовщину: темная, возможно, опасная, и абсолютно не понятная. После чтения такой литературы довольно сложно сделать какие-либо выводы.

Второй жанр совершенно другой, но столь же «полезный», написанный экспертами, для того, чтобы произвести впечатление на других экспертов. Эта жанр характеризуется употреблением таких терминов как машина Тьюринга, имя Ричарда Фейнмана, Гильбертово пространство и преобразование Адамара, все вышеупомянутое и еще примерно 75 слов, за которыми следует путаница уравнений с незнакомой и необъяснимой терминологией. Конечно же, вы все хорошо помните, что означает |0>!

Три параллельные вселенные

Одной из причин, почему эта тема настолько сложна, является то, что квантовые вычисления охватывают три дисциплины с очень разной терминологией и интересами. Все началось с физиков-теоретиков. Еще в 1980 году физик Пол Бениофф (Paul Benioff) из Национальной Аргоннской лаборатории описал, как некоторые квантовомеханические эффекты могут быть использованы для реализации машины Тьюринга. Два года спустя известный физик Ричард Фейнман также поднял вопрос о компьютере с использованием квантового поведения.

Но идея была подхвачена совершенно другой группой: компьютерными специалистами и математиками. Взяв из физики основные идеи квантового бита (кубита) и обратимых унитарных преобразований (которые они называли квантовыми вентилями или кувентилями), компьютерные специалисты изучили, какие вычисления могли бы быть выполнены, если бы существовали идеальные кубиты и квантовые вентили. Они обнаружили случаи, когда такие предполагаемые компьютеры могли быть намного быстрее, чем обычные цифровые компьютеры.

Этот результат побудил физиков-экспериментаторов – третью группу – начать попытки по созданию физических устройств, которые могли бы быть приближенны к идеальным кубитам и квантовым вентилям. Это были долгие, ресурсоемкие исследования, которое до сих пор не доказали, что реально работающий квантовый компьютер физически возможен. Но такая возможность чрезвычайно обнадеживает.

Некоторые пояснения

Итак, что это за воображаемый компьютер, который нас интересует? Давайте сначала проясним некоторые недоразумения. Квантовый компьютер не является обычным компьютером, имитирующим квантовомеханические явления. Также это и не обычный цифровой компьютер, построенный из некоторых транзисторов (эпохи окончания закона Мура), настолько крошечных, что они хранят или переключают отдельные кванты энергии.

Вместо этого, квантовые компьютеры – это машины, основанные на уникальном поведении, описываемом квантовой механикой, и совершенно отличающимся от поведения классических систем. Одно из таких отличий – способность частицы или группы частиц в некотором отношении находиться только в двух дискретных квантовых базовых состояниях – назовем их 0 и 1. Мы обойдемся здесь без забавных скобок (обозначений принятых в квантовой теории – добавлено переводчиком) Примерами такого рода могут быть спин электрона, поляризация фотона или заряд квантовой точки.

Во-вторых, квантовые вычисления зависят от свойства суперпозиции – контринтуитивной способности частицы находиться в некоторой  комбинации обоих базовых состояниях 0 и 1 одновременно, до тех пор, пока не произведено измерение. Как только вы измеряете такое состояние, оно превращается в 0 или 1, и вся остальная информация исчезает. Квантовая механика правильно описывает такое комбинированное состояние как сумму двух базовых состояний, каждое из которых умножается на некоторый комплексный коэффициент. Полная величина этих коэффициентов всегда равна 1. Такое состояние можно представить как единичный вектор, начинающийся в начале координат и заканчивающийся где-то на сфере,  называемой сферой Блоха, которая приведена на рисунке 2. Ключевым моментом здесь является то, что квадрат (модуля – добавлено переводчиком) комплексного коэффициента для  базового состояния 0 представляет вероятность того, что в результате измерения кубит будет обнаружен  в  базовом состоянии 0, аналогично для  базового состояния 1. И когда вы производите измерение, вы всегда получите  или точно состояние 0, или точно состояние 1.

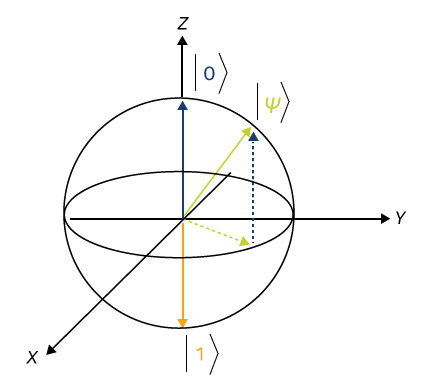
Это (свойство суперпозиции – добавлено переводчиком) важно, потому что позволяет кубиту быть в обоих состояниях 0 и 1 одновременно. Следовательно, регистр, состоящий из n кубит, может одновременно «содержать» все возможные двоичные числа n бит длиной. Это позволяет квантовому компьютеру выполнять одну операцию не только с одним n-разрядным целым числом, но и со всеми возможными n-разрядными целыми числами сразу – очень существенный параллелизм по мере увеличения n.

В-третьих, квантовые вычисления зависят от способности квантового вентиля изменять эти коэффициенты и, следовательно, вероятность измерения какого-либо определенного числа – предсказуемым образом. Если вы начинаете с состояния, в котором все коэффициенты во всех кубитах равны, а затем измерите все кубиты в регистре, вы равновероятно найдете любую строку бит между строкой из одних нулей и строкой из одних единиц, включительно. Но запустив это начальное состояние через тщательно подобранную последовательность квантовых вентилей, квантовый компьютер может изменить эти коэффициенты так, что состояние, которое вы наиболее вероятно измерите на выходе, будет представлять собой результат некоторого вычисления, например, весьма вероятно, что вы измерите биты числа, которое является точным квадратом.

Компьютер на бумаге

Но какое отношение все это имеет к реальным вычислениям? Чтобы ответить на этот вопрос, мы должны перенести наше внимание с физиков-теоретиков на компьютерных специалистов и математиков. Чтобы получить практические результаты, мы должны иметь возможность перевести регистр кубитов в определенную суперпозицию состояний. Нам нужны квантовые вентили, возможно, провода и какие-то устройства вывода результатов.

Все это легко для компьютерных специалистов – они просто могут предположить, что эти идеи уже воплощены в реальной жизни. Однако им придется пойти на уступки квантовой механике. Чтобы не нарушить законы квантовой физики, компьютерные специалисты должны потребовать, чтобы квантовые вентили были обратимы – вы можете поместить результат на выход и получить правильные входные значения на входе. И они настаивают на том, чтобы квантовые вентили были унитарными преобразованиями. В соответствии с матричной алгеброй, это означает, что, когда вы пропускаете состояние кубита через квантовый вентиль, состояние, которое вы получите, даст при измерении либо 0, либо 1, а сумма вероятностей из квадратов (модулей – добавлено переводчиком) этих коэффициентов останется равной единице.

Обратите внимание, что эти квантовые вентили, даже в теории, очень не похожи на обычные логические элементы. Например, большинство булевых функций не обратимы. Невозможно вывести входные данные с логического элемента И-НЕ, если выход не будет равен 0. И, конечно, логические элементы работают только с единицами и нулями (состояниями 1 и 0), в то время как квантовые вентили работают, вращая вектор внутри сферы Блоха. На самом деле между ними не существует ничего общего кроме названия.

Компьютерные специалисты выяснили, что для эмуляции машины Тьюринга достаточно очень небольшого набора квантовых вентилей – всего лишь набор одновходовых квантовых вентилей и один двухвходовой квантовый вентиль. Наиболее часто используемым примером двухвходового квантового вентиля является «контролируемое НЕ» (Сontrolled NOT – CNOT). Эта обратимая функция либо переворачивает векторное состояние кубита, либо оставляет его неизменным, в зависимости от состояния второго кубита. Это скорее похоже на квантовую аналогию с «исключающим ИЛИ».

Возможные преимущества

Мы все еще не ответили на вопрос, как все это можно использовать. Ответ заключается в том, что если вы соедините подходящим образом достаточное количество квантовых вентилей вместе, и если вы можете приготовить входные кубиты представляющие все возможные числа в вашей области входных данных, тогда на выходе массива квантовых вентилей вы, теоретически, можете измерить биты, которые представляют значения некоторой полезной функции.

Приведем пример. В 1994 году математик Питер Шор, в Bell Labs, разработал алгоритм факторизации (разложения на простые сомножители – добавлено переводчиком) очень больших чисел с использованием квантовых подпрограмм. Такая факторизация является жизненно важной проблемой в прикладной математике, потому что не существует аналитического решения: единственный способ – метод проб и ошибок, и вы можете всего лишь сделать алгоритм быстрее, выбрав более искусным образом соответствующие пробные числа. Соответственно, когда вы делаете входное число очень большим, количество проб и ошибок становится огромным. Не случайно это является основой алгоритмов криптографии, подобных RSA. RSA и шифры на основе эллиптических кривых трудно взломать, особенно потому, что так трудно факторизовать огромные числа.

Алгоритм Шора объединил некоторые традиционные вычисления с двумя квантовыми функциями, которые непосредственно ускоряют алгоритм в части метода проб и ошибок, по сути, перебирая все возможные числа в одно и то же время, демонстрация работы алгоритма приведена на рисунке 3. Одна из этих квантовых функций выполняет модульное возведение в степень, а другая осуществляет квантовую версию быстрого преобразования Фурье (БПФ). По причинам, которые мог бы полюбить только математик, если бы мы ввели набор из n кубитов, подготовленных так, что вместе они представляют все возможные двоичные числа до длины n, то в квантовых вентилях различные состояния в суперпозиции взаимно компенсируют друг друга – подобно интерференции двух когерентных световых лучей – и мы остаемся с определенной структурой состояний в выходном регистре.

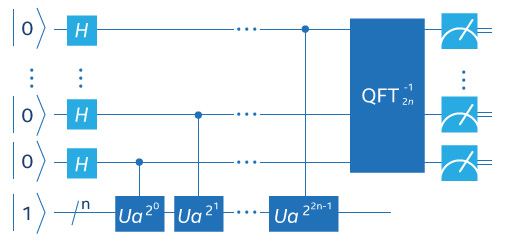
Эта процедура не дает простой множитель – это лишь промежуточный шаг, который позволяет вычислить возможный простой множитель. Такое расчет выполняется путем измерения кубитов, – отметим, что здесь мы находимся в области возможности, но не точности, измерения наиболее вероятного состояния каждого кубита – а затем, чтобы убедиться в правильности результата, необходимо произвести множество обычных вычислений на обычном процессоре (CPU).

Все это может показаться безнадежно сложным и неосуществимым. Но способность квантового возведения в степень и квантового БПФ работать одновременно со всеми возможными степенями числа 2, чтобы найти наибольший простой множитель, делает алгоритм Шора быстрее, чем обычные вычисления для больших чисел, даже при использовании довольно медленных теоретических квантовых подпрограмм.

Алгоритм Шора являет собой яркий образец квантовых вычислений, потому что он одновременно не похож на обычные вычисления и потенциально чрезвычайно важен. Но он не одинок. Национальный институт стандартов и технологий США (NIST) поддерживает большую библиотеку алгоритмов квантовых вычислений в своем Зоопарке Квантовых Алгоритмов, по адресу math.nist.gov/quantum/zoo/.

Являются ли эти алгоритмы просто математическими упражнениями? Пока еще слишком рано это утверждать. Но на практике исследователи действительно создали лабораторные квантовые калькуляторы с несколькими рабочими кубитами. Эти машины успешно разложили на простые множители число 15 (впервые это было сделано в IBM в 2001 году), вполне ожидаемо получив в результате 3 и 5, а текущий мировой рекорд составляет число 21 (сделано объединенной командой из нескольких институтов в 2012 году). Так что для небольших чисел идея работает. Пригодность такого подхода для больших чисел можно будет проверить только в будущем на машинах с большим количеством кубитов. И это переносит вопрос в практическую плоскость.

Путь к реализации

Для создания работоспособных квантовых вычислительных устройств необходимо пройти ряд этапов реализации. Мы должны построить рабочие кубиты – не только пять, но тысячи. Мы должны организовать структуру из  квантовых вентилей и эквивалент проводов – если только мы не сможем заставить вентили действовать непосредственно на состояние во входном квантовом регистре. Все это сложные задачи, и график их решения непредсказуем.

К сожалению, проблемы связаны не столько с новизной проблем, сколько с законами квантовой механики и классической физики. Возможно, самая главная и наименее знакомая из них, называется декогеренцией. Роль кубит состоит в том, чтобы удерживать физический объект – например, ион, пакет фотонов или электрон — на месте, чтобы мы могли воздействовать на него и в конечном итоге измерять квантованную величину, такую как заряд или спин. Чтобы эта величина вела себя квантовым, а не классическим образом, мы должны иметь возможность ограничить ее состояние суперпозицией двух чистых базовых состояний, которые мы называли 0 и 1.

Но природа квантовых систем такова, что связывает их с вещами вокруг них, значительно увеличивая количество возможных базовых состояний. Физики называют такое размытие чистых состояний декогеренцией. Аналогией может быть когерентный лазерный луч в световоде, рассеивающийся на неоднородностях материала и размывающейся от суперпозиции двух мод в полностью некогерентный свет. Задачей создания физического кубита является как можно дольше предотвращать декогеренцию.

На деле это означает, что даже один кубит это сложный лабораторный инструмент, возможно, с использованием лазеров или высокочастотных радиопередатчиков, точно контролируемые электрические и магнитные поля, точные размеры, специальные материалы и, возможно, криогенное охлаждение. Его использование, по сути, является сложной экспериментальной процедурой. Даже при всех этих усилиях, сегодня это «как можно дольше» измеряется десятками микросекунд. Таким образом, у вас очень мало времени для выполнения квантовых вычислений, до того, как ваши кубиты потеряют свою согласованность. То есть, до того как информация исчезнет.

Сегодня эти ограничения исключают возможность больших квантовых регистров или проведения вычислений, для которых требуется более нескольких микросекунд. Тем не менее, в настоящее время в микроэлектронике ведутся исследования по созданию гораздо более обширных массивов кубитов и квантовых вентилей.

Однако сама эта работа несколько бессвязна, потому что пока нет определенности в отношении того, какое физическое явление использовать для хранения квантовых состояний. Существуют конструкции кубит, которые квантуют поляризацию фотонов, заряд электронов, захваченных квантовыми точками, чистый спин сверхохлажденных ионов в ловушке, заряд в устройстве, называемом трансмоном, и некоторые другие подходы.

Тип кубита, который вы выберете, естественно определит реализацию квантовых вентилей. Например, вы можете использовать взаимодействие радиоимпульсов с внутренними спинами в молекулах в ловушке или взаимодействие расщепителей пучков с фотонными модами в волноводах. Очевидно, что существо дела находится  глубоко в области экспериментальной физики. И, как уже упоминалось, реализация кубитов или квантовых вентилей требует использования большого количества различного оборудования, от цифровой логики до лазеров или радиопередатчиков, антенн и до криогенных охладителей.

Реализация кубит также зависит, от того каким образом измеряется состояние кубит. Вам может потребоваться сверхчувствительный фотометр или болометр, мост сопротивлений или какое-либо другое невероятно чувствительное устройство для измерения кубитов и перевода состояния суперпозиции в базовое состояние. И, кроме того, этот процесс измерения состояния кубит вызывает еще одну проблему, незнакомую традиционным вычислениям: получение неправильного ответа.

Сомнения

Существует два основных типа проблем с извлечением базового состояния из кубита. Во-первых, вы измеряете квантовую суперпозицию, а не классическую величину. Предполагая, что кубит остался когерентным, вы получите одно или другое из базовых состояний, но вы не можете заранее быть уверены какое именно из них вы получите: вы можете быть уверены только в том, что вероятность того, что вы получите определенное состояние, будет квадратом (модуля – добавлено переводчиком) коэффициента этого состояния в суперпозиции. Если вы измеряете кубит в точно таком же состоянии сто раз, вы получите распределение нулей и единиц, которое сходится к квадратам (модулей) коэффициентов.

Таким образом, вы не знаете, действительно ли то базовое состояние, которое вы измерили в некоторой  попытке, имеет наибольшую вероятность. После того, как вы считали квантовый выходной регистр, измерив биты, тем самым установив их все в базовые состояния – у вас есть три варианта. Вы можете усомниться, что у вас есть правильный ответ и продолжить дальше. Вы можете проверить традиционными вычислениями, как это делает алгоритм Шора, чтобы узнать, действительно ли число, которое вы считали, является правильным решением. Или же, вы можете повторить вычисление большое количество раз, последовательно или параллельно, и взять наиболее часто встречающийся результат. Также можно организовать свои вычисления таким образом, чтобы ответом было распределение вероятностей базовых состояний, а не конкретное двоичное число. В этом случае также необходимо повторение..

Это верно даже для теоретически совершенного квантового компьютера. Но в действительной реализации есть еще одна проблема: старый добрый классический шум. Даже если все идет хорошо, нет декогеренции кубитов, и вычисление предназначено для получения ответа с очень высокой вероятностью, вы все еще наблюдаете за кубитами, пытаясь измерить очень и очень маленькие физические величины. Шум все равно присутствует. Опять же, единственным решением является либо обнаружение ошибки путем дальнейших вычислений, либо выполнение вычислений столько раз, что вы готовы принять любую оставшуюся в результате этого неопределенность. Концепция гарантированного правильного ответа чужда самой сути квантовых вычислений.

Если все это не рисует розовую картину будущего квантовых вычислений, то к этому следует отнестись очень серьезно. Идут поиски наилучшего выбора для реализации  кубитов, хотя ответ может оказаться зависящим от алгоритма. Специалисты по микроэлектронике работают над миниатюризацией квантовых компонентов на основе новых материалов и структур, которые позволили бы создавать очень большие массивы квантовых вычислительных устройств, и которые могли бы массово производиться подобно чипам традиционных процессоров. Компьютерные специалисты разрабатывают прототипы ассемблеров и компиляторов, которые могут преобразовать алгоритм в расположение квантовых регистров и  квантовых вентилей в конкретной технологии.

Стоит ли оно того? Вот один факт. Шор подсчитал, что скромный гибридный, то есть квантовый плюс обычный, компьютер может взломать мощный алгоритм шифрования RSA быстрее, чем обычный компьютер может его зашифровать. Были получены аналогичные результаты для таких задач, как сортировка и распутывание других аналогичных сложных математических задач. Итак, в этой области присутствует достаточно перспектив, чтобы исследователи не теряли энтузиазм. Но было бы неплохо увидеть все это еще при жизни.

Источник статьи: Who Cares About Quantum Computing?